本文是对《Diffusion Policy: Visuomotor Policy Learning via Action Diffusion》的学习记录与详解

Diffusion Policy 论文精读：从Diffusion到Policy

本文是对《Diffusion Policy: Visuomotor Policy Learning via Action Diffusion》的学习记录与详解。本文主要回顾了Diffusion Model，然后介绍了Diffusion Policy的原理。以下是原论文的链接：

Diffusion Policy: Visuomotor Policy Learning via Action Diffusion

Diffusion Model

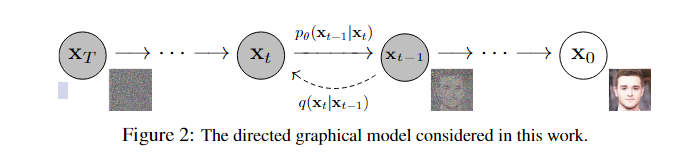
Diffusion Model的核心思想是逐步向数据添加噪声，并学习如何逆转这一过程以恢复原始数据。这一过程通常包括前向扩散（Forward Diffusion，上图由右到左的过程） 和 反向扩散（Reverse Diffusion，上图由左到右的过程） 两个阶段。

Diffusion 前向过程

Diffusion 前向过程是逐步向数据添加高斯噪声，使其在足够多步后变成一组接近标准高斯分布的噪声。我们设原始图片$x_0 \sim q(x_0)$，然后逐步添加高斯噪声，得到$x_1, x_2, \cdots, x_T$，其中$x_t$是第$t$步添加噪声后的图片，$t$从$1$到$T$，显然，在前向过程中，$t$时刻的分布只与$t-1$时刻的分布有关，因此，可以将前向过程视作一个马尔可夫过程:

\[q(x_t|x_{t-1}) = \mathcal{N}(x_t; \sqrt{1-\beta_t} x_{t-1}, \beta_t I) \tag{1-1}\]

其中，$\beta_t$是一个控制高斯分布方差的超参数$\beta_t \in (0, 1)$。 在式(1-1)中，我们从一个高斯分布中采样得到$x_t$，但这个过程是无法进行反传梯度的，为此我们需要用到一个很关键的技巧：重参数化技巧（Reparameterization Trick）。

重参数化技巧

重参数化技巧的目的是将随机变量从高斯分布中分离出来，使得我们可以对随机变量进行反传梯度。具体来说，我们可以将随机变量表示为：

\[x_t = \sqrt{1-\beta_t} x_{t-1} + \sqrt{\beta_t} \epsilon_t \tag{1-2}\]

这样一来，我们就可以将变量$x_t$从高斯分布中分离出来，使得我们可以对其进行反传梯度。但是，在式(1-2)中，想要得到$x_t$，我们必须从$x_0$开始，一步步计算到$x_t$，这显然是非常耗时的。因此，我们希望给定$x_0$和$t$，能够直接得到$x_t$。为了方便起见，我们设$\alpha_t = 1-\beta_t$，$\bar{\alpha}t = \prod{i=1}^t \alpha_i$，则式(1-2)可以改写为：

\[x_t = \sqrt{\alpha_t} x_{t-1} + \sqrt{1-\alpha_t} \epsilon_t \tag{1-3}\]

进一步，我们将$x_{t-1}$展开：

\[x_t = \sqrt{\alpha_t} \sqrt{\alpha_{t-1}} x_{t-2} + \sqrt{\alpha_t} \sqrt{1-\alpha_{t-1}} \epsilon_{t-1} + \sqrt{1-\alpha_t} \epsilon_t \\\]

其中，$\epsilon_t \sim \mathcal{N}(0, I)$，$\epsilon_{t-1} \sim \mathcal{N}(0, I)$。由独立高斯分布的可加性，我们得到：

\[x_t = \sqrt{\alpha_t \alpha_{t-1}} x_{t-2} + \sqrt{1-\alpha_t \alpha_{t-1}} \bar{\epsilon}_t \\\]

其中，$\bar{\epsilon}_t \sim \mathcal{N}(0, I)$。同理，我们不难写出：

\[x_t = \sqrt{\bar{\alpha}_t} x_0 + \sqrt{1-\bar{\alpha}_t} \epsilon_t \tag{1-4}\]

式(1-4)就是我们想要的，给定$x_0$和$t$，直接得到$x_t$的表达式。

Diffusion 反向过程

反向过程顾名思义就是从一堆高斯噪声中逐步恢复出原始图像信息。从理论上来说，如果我们能够逆转每一个添加噪声的过程，即得到分布$q(x_{t-1}|x_{t})$，那么我们就可以从$x_T$逐步恢复出$x_0$。我们利用深度神经网络强大的函数拟合功能，训练一个模型$p_\theta(x_{t-1}|x_t)$，使得$p_\theta(x_{t-1}|x_t)$尽可能接近$q(x_{t-1}|x_t)$，即

\[p_\theta(x_{t-1}|x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \Sigma_\theta(x_t, t)) \tag{1-5}\]

训练的关键在于如何选择合适的$\mu_\theta(x_t, t)$和$\Sigma_\theta(x_t, t)$，这也是我们模型训练的关键。利用贝叶斯公式，在$x_0$已知的情况下，我们可以得到：

\[\begin{aligned} p_\theta(x_{t-1}|x_t) &= q(x_{t-1}|x_t, x_0) = \frac{q(x_t|x_{t-1})q(x_{t-1}|x_0)}{q(x_t|x_0)} \\ &= \frac{\mathcal{N}(x_t; \sqrt{\alpha_t} x_{t-1}, (1-\alpha_t) I) \mathcal{N}(x_{t-1}; \sqrt{\bar{\alpha}_{t-1}} x_0, (1-\bar{\alpha}_{t-1}) I)}{\mathcal{N}(x_t; \sqrt{\bar{\alpha}_t} x_0, (1-\bar{\alpha}_t) I)}\\ &\propto exp(-\frac{1}{2}(\frac{(x_t - \sqrt{\alpha_t} x_{t-1})^2}{1-\alpha_t} + \frac{(x_{t-1} - \sqrt{\bar{\alpha}_{t-1}} x_0)^2}{1-\bar{\alpha}_{t-1}}-\frac{(x_t - \sqrt{\bar{\alpha}_t} x_0)^2}{1-\bar{\alpha}_t}))\\ &= exp(-\frac{1}{2}((\frac{\alpha_t}{1-\alpha_t}+\frac{1}{1-\bar{\alpha}_{t-1}})x_{t-1}^2-(\frac{2\sqrt{\alpha_t}}{1-\alpha_t}x_t+\frac{2\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}}x_0)x_{t-1}+C(x_t, x_0))) \end{aligned}\]

由于高斯分布的概率密度函数为： \(p(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \propto exp(-\frac{1}{2}(\frac{1}{\sigma^2}x^2-2\frac{\mu}{\sigma^2}x+\frac{\mu^2}{\sigma^2}))\)

对比可得：

\[\begin{aligned} \frac{\alpha_t}{1-\alpha_t}+\frac{1}{1-\bar{\alpha}_{t-1}} &= \frac{1}{\sigma^2} \\ -\frac{2\sqrt{\alpha_t}}{1-\alpha_t}x_t+\frac{2\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}}x_0 &= -\frac{2\mu}{\sigma^2} \\ \end{aligned}\]

即：

\[\sigma^2 = \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \beta_t \\ \begin{aligned} \mu &= \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}x_t+\frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t}x_0 \\ &\overset{式1-4}{=} \frac{1}{\sqrt{\alpha_t}}(x_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_t) \\ \end{aligned}\]

则式1-5中的$\mu_\theta(x_t, t)$和$\Sigma_\theta(x_t, t)$可以表示为：

\[\mu_\theta(x_t, t) = \frac{1}{\sqrt{\alpha_t}}(x_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_\theta(x_t, t)) \\ \Sigma_\theta(x_t, t) = \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \beta_t\]

在DDPM中，作者认为由于$\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \approx 1$，因此可以简化为$\beta_t$，即：

\[\Sigma_\theta(x_t, t) = \beta_t\]

Diffusion model 训练和采样

由上述推导我们可以看出，Diffusion Model 的关键在于训练噪声预测的模型$\epsilon_\theta(x_t, t)$，DDPM采用了一个简化的损失函数：

\[L = \mathbb{E}_{x_0, t,\epsilon}[\| \epsilon - \epsilon_\theta(\sqrt{\bar{\alpha}_t} x_0 + \sqrt{1-\bar{\alpha}_t} \epsilon_t, t) \|^2]\]

DDPM认为方差可以用$\beta_t$来近似，因此不需要额外训练一个用于预测方差的模型。

训练过程如下图所示：

采样过程如下图所示：

Diffusion Policy

上文中我们分析并推导了diffusion的基本原理，简单来说，就是通过学习一个噪声预测模型，来预测从原始数据逐步添加噪声到完全高斯分布的噪声，然后通过训练好的模型，从高斯分布中采样得到原始数据，以达到生成的效果。而Diffusion Policy则是将diffusion的思想应用到机器人的策略生成上。在Diffusion Policy之前，有一篇重要的工作也值得我们关注，这篇工作包含了Diffusion Policy的雏形和重要思想。

Diffuser

Planning with Diffusion for Flexible Behavior Synthesis

我们首先从离线强化学习出发，离线强化学习希望从已有的数据中学习到一个最优的策略，使其能够直接部署到环境中并获得不错的收益。原论文首先将每一条轨迹写成如下形式：

\[\tau = \begin{bmatrix} s_0 & s_1 & \cdots & s_T \\ a_0 & a_1 & \cdots & a_T \end{bmatrix}\]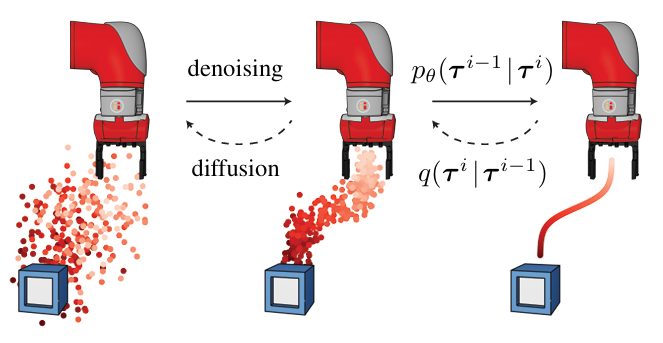

从上图我们可以看出，Diffuser将轨迹看作是状态和动作的序列，然后通过diffusion模型来生成轨迹，基本原理与Diffusion Model是一致的。

在路径规划上，由于Diffusion的原理，整个生成过程并不强调自回归或马尔可夫性，而是通过迭代地对包含可变数量的状态-动作对去噪从而采样计划中的轨迹。简单来说，该模型是首先生成一个大致的规划，然后逐步通过去噪来细化规划，直到生成出一条完整可用的轨迹，模型的示意图如下：

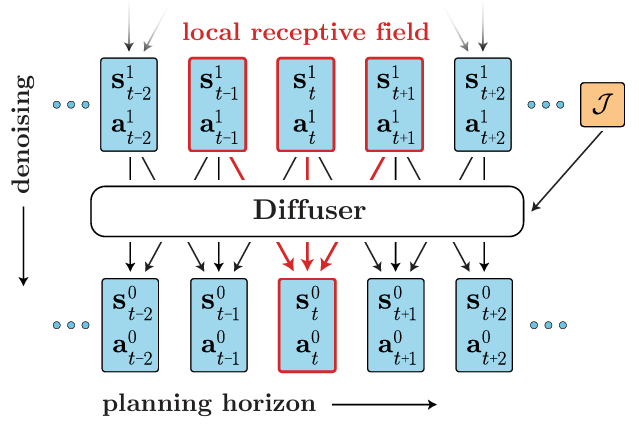
但在具体实践中，我们会遇到一些问题。首先，原始的Duffusion Model只能生成与原始数据分布类似的轨迹，但是无法确保生成出的轨迹是满足要求的，即生成的轨迹不一定能够达到目标或满足一定的条件约束。

利用扩散模型进行规划（Guided Diffusion Planning）

为了解决上述的问题，文中引入了一个布尔型的变量来表示轨迹是否是最优的。假设$\mathcal{O}_t$是一个二元随机变量，表示第$t$步的轨迹是否是最优的，其中$p(\mathcal{O}_t=1) = exp(r(s_t, a_t))$。我们希望采样到的最优轨迹应该满足每一个时间步的$\mathcal{O}_t$都为1，则最优轨迹的分布可以表示为：

\[\hat{p}_\theta(\tau) = p(\tau |\mathcal{O}_{1:T}=1) \propto p(\tau)p(\mathcal{O}_{1:T}=1|\tau) \tag{2-1}\]

至此，我们已经把轨迹的生成问题转换为了一个条件概率的生成问题，我们接下来只需要让扩散模型在该分布下采样即可。训练模型的目的就是最大化式(2-1)的对数似然，我们对式(2-1)两边取对数后求导，令：

\[\begin{aligned} g &= \nabla_{\tau} p(\mathcal{O}_{1:T}=1|\tau)|_{\tau = \mu} \\ &= \Sigma_{t=0}^{T} \nabla_{s_t,a_t} r(s_t, a_t)|_{(s_t, a_t) = \mu_t} \\ &= \nabla \mathcal{J}(\mu) \end{aligned} \tag{2-2}\]

反向过程可以近似如下：

\[p_\theta(\tau^{i-1}|\tau^i,\mathcal{O}_{1:T}=1) = \mathcal{N}(\tau^{i-1};\mu_\theta(\tau^i,i)+\Sigma g, \Sigma_\theta(\tau^i,i)) \tag{2-3}\]

其中，$\mu_\theta(\tau^i,i)$和$\Sigma_\theta(\tau^i,i)$是原始扩散模型的反向过程中的均值与方差。将式(2-3)与式(1-5)对比，我们可以看出，实际上就是在原来的均值的基础上加了一项$\Sigma g$作为优化项。于是，我们得到Guided Diffusion Planning的算法流程如下图所示：

Diffusion Policy

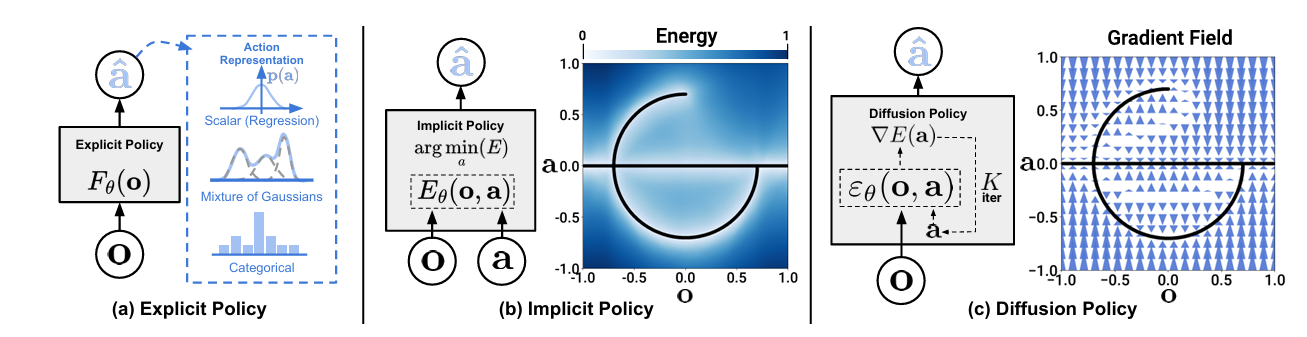
为什么需要Diffusion Policy

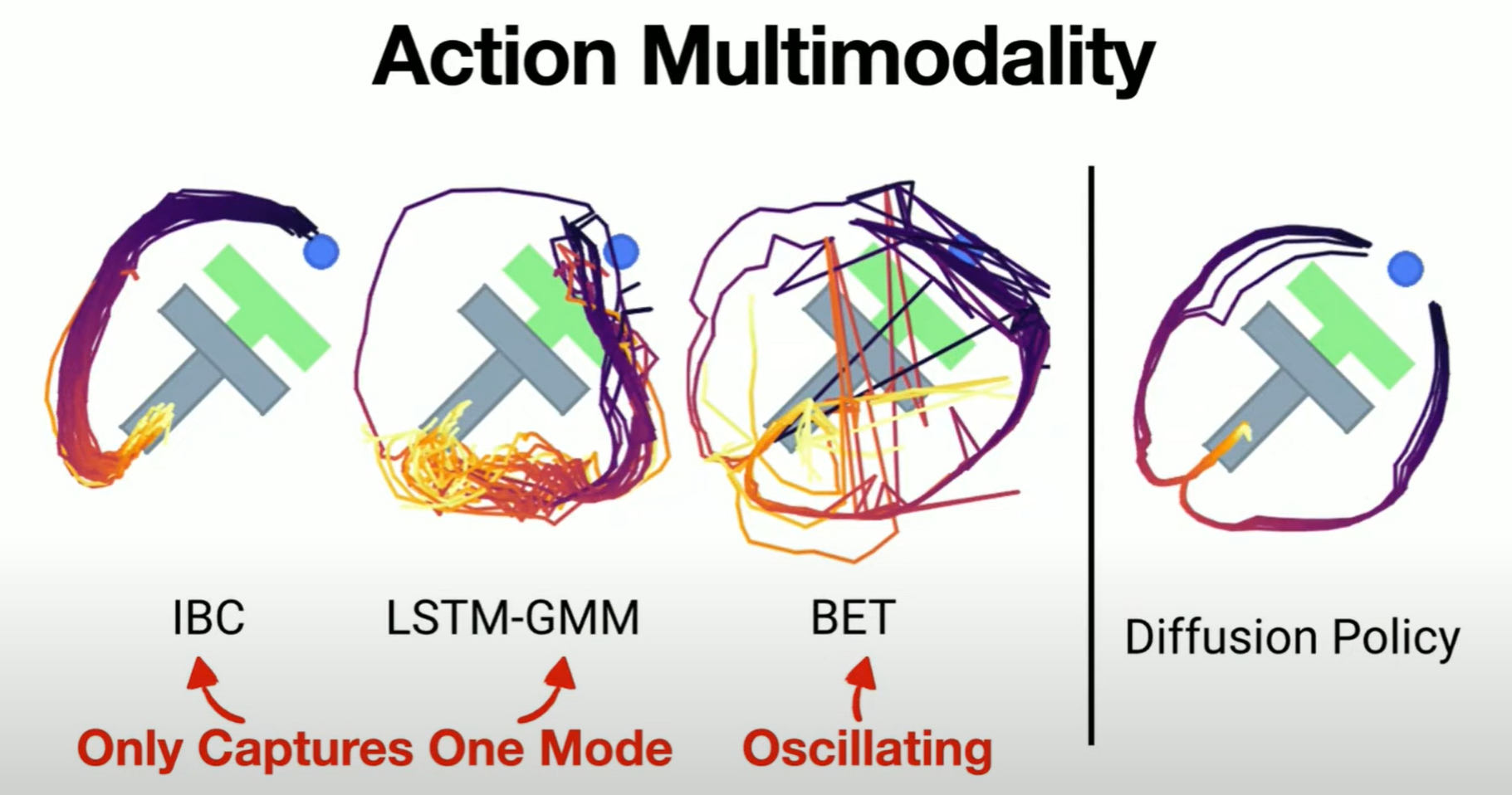
作者在指出，Diffusion Policy首先解决的是Multi-Modal(多模态)的问题。我们知道，传统的前馈神经网络相当于一个函数，对于给定的输入，只会有一种可能的输出。但是，在实际数据中，解决同一个问题可能具有不同的方法。例如，假设现在有100名司机开车经过一棵大树，可能有50名司机选择向左绕开，另外的50名司机选择向右绕开。如果使用传统的前馈神经网络进行训练，为了最小化损失函数，模型可能会倾向于选择这两条路径的中间值，这样就会导致模型学习到完全错误的策略。因此，我们需要引入概率分布，使得网络成为一个对于相同的输入可以有多个不同输出的函数，极大提高了灵活性。

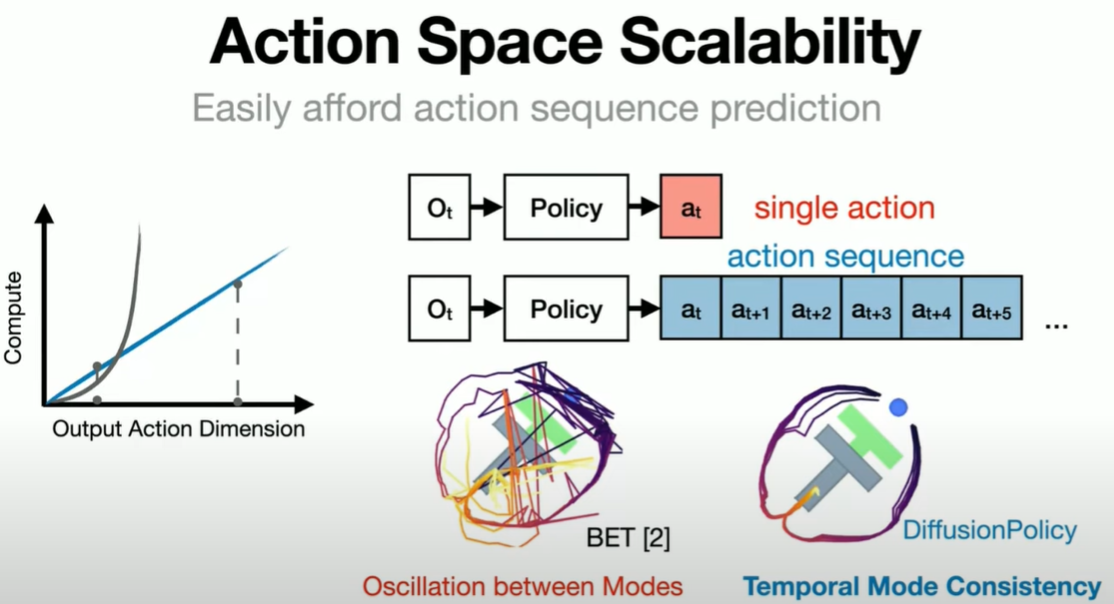
另一个解决的是Action Space Scalability的问题。与Diffuser类似，模型在进行策略预测时会生成多步的动作而不是仅关注眼前的一两步，使得动作更加具有连贯性（在时间上具有一致性）。作者指出，现在的动作预测主要有两种思路：一种是在连续空间中预测（类似回归任务），一种是将动作空间分成若干区间，进行离散预测（类似分类任务）。在进行Multi-Modal Action Prediction的任务时，人们倾向于将采用离散预测的方式。例如，继续沿用上述开车的例子，我们可以把方向盘的运动角度均匀划分为100个区间，这样就将连续的角度预测转换为一个100分类的问题。可以预见的是，这种方法会随着预测步数的增多维度会呈指数级增长，另外，在实际应用中，预测一个六自由度的机械臂的一步动作就已经有很高的维度了，因此，这种离散预测的方法无法胜任复杂的控制。Diffusion Policy追求的是不仅可以预测每一步，而且可以在高维连续控制中实现。对于我们来说，我们可以直接预测未来每一步，无论是接下来的20步还是100步，是向左还是向右，而不是在每一步预测之后再执行，再决定下一步该怎么走。

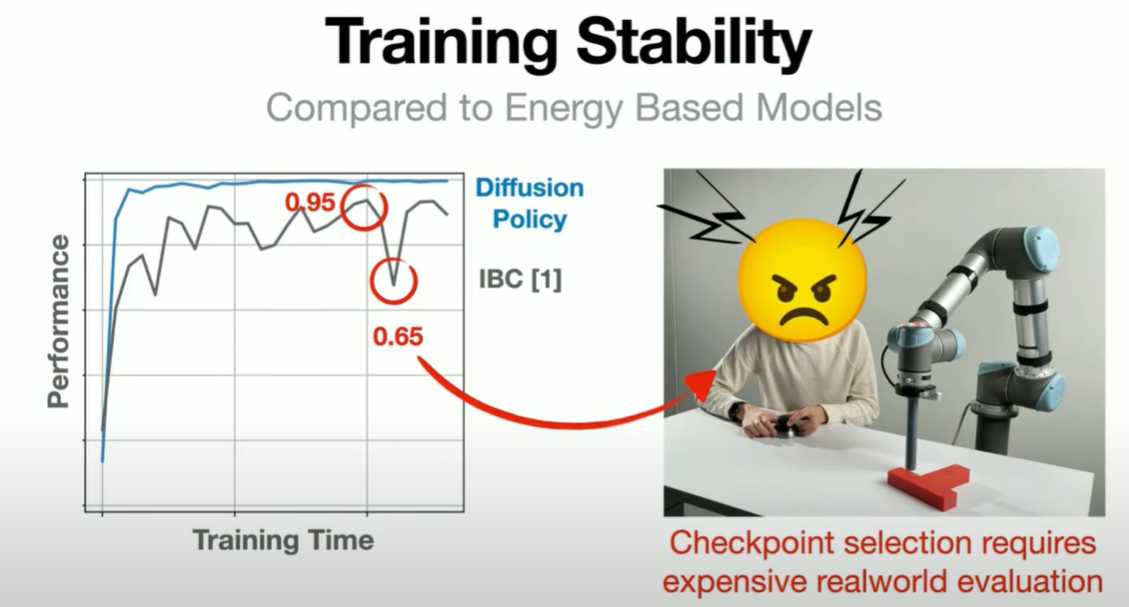
最后是Training Stability的问题，作者指出Diffusion方法的强大之处在于，它的性能不逊色于GAN，但其训练过程非常稳定。基本上，你可以随便调整参数，生成器就能够输出结果，可能效果不是最优的，但基本上都能work。

Diffusion Policy原理

文中沿用了DDPM的方法，将去噪过程表示为：

\[x^{k-1} = \alpha(x^k - \gamma\varepsilon_\theta(x^k,k)+\mathcal{N}(0,\sigma^2I)) \tag{3-1}\]

训练过程为：

\[\mathcal{L} = MSE(\varepsilon^k,\varepsilon_\theta(x^0 + \varepsilon^k,k)) \tag{3-2}\]

在实际应用中，作者将$A_t$和$O_t$建模为条件概率分布，即$p(A_t \mid O_t)$，于是，上式可以修改为：

\[A^{k-1}_t = \alpha(A^k_t - \gamma\varepsilon_\theta(A^k_t,O_t,k)+\mathcal{N}(0,\sigma^2I)) \tag{3-3}\] \[\mathcal{L} = MSE(\varepsilon^k,\varepsilon_\theta(O_t, A^0_t + \varepsilon^k,k)) \tag{3-4}\]